Motivation
Direct Statistical Simulation is a relatively new and very promising technique for understanding the long-term statistical properties of highly turbulent, anisotropic flow. Anisotropic flow occurs in astrophysical and geophysical contexts in a number of guises: the zonal jets found on Jupiter and Saturn, the mean dynamo-generated magnetic fields on solar-type and fully convective M-dwarfs, and the quasi-biennial oscillation on Earth. DSS has been extensively verified and tested against many problems in atmospheric science \citep{2008JAtS…65.1955M}, wall-bounded shear flows \citep{2017RSPTA.37560081F}, and the magnetorotational dynamo \citep{2015PhRvL.114h5002S}.
The basic mathematical idea behind DSS is simple: rather than evolve the fluid variables (velocities, magnetic fields, etc), instead one evolves their statistics. These statistics, represented in DSS by cumulants of the flow variables, are typically much smoother than the variables themselves. This means they can be represented with far fewer spatial grid points. In addition, by directly simulating the statistics, one can find variances without having to run a DNS long enough to build up robust correlations.
We are interested in studying a series of instabilities that lead to anisotropic flows. Our prototype problem is the Busse Annulus, a simple model for convection in a rapidly rotating annulus. The annulus considers the duct on the right, a cross section cut from between the two concentric cylinders on the left,
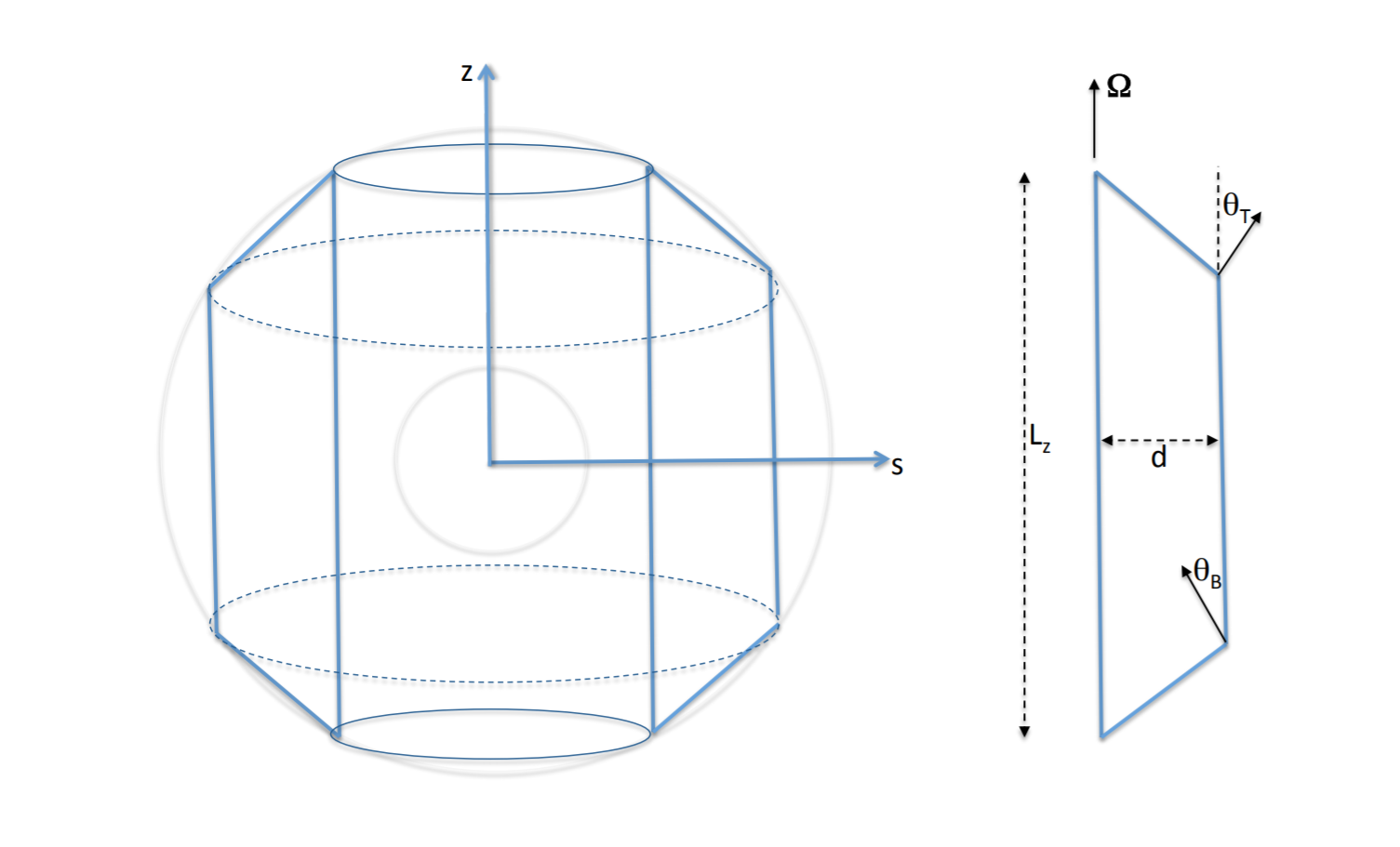
In order to consier non-axisymmetric effects in the rapidly rotating domain (with rotation rate Ω about z), a small part of the azimuthal direction is retained, while we integrate down the z direction. This leaves us with a two dimensional, Cartesian domain in x and y, representing a small piece of the radial and azimuthal directions, respectively.
Methods
We’ve developed a set of operators for Dedalus that implement the necessary projections and symmetrizations required for performing these calculations in an efficient manner. Because we are performing zonal averages in order to construct the cumulants, the dimension of each cumulant is different: the first cumulant for a 2D domain is 1D, but the second cumulant is 3D. However, in its current version, Dedalus must have all fields be the same dimension for a given problem. We’ve developed a set of operators to project a 1D field stored within a 3D data structure. These operators work for arbitrary bases, allowing us to use the parity (sin/cos) bases best suited to the boundary conditions of the Busse annulus.
Project Repository
Follow along at at Github!
External Collaborators
- Steve Tobias, Leeds
- Brad Marston, Brown
- Keaton Burns, Flatiron Institute