…or how six months in the lab can save you an hour in the library.
For the 2022-2023 year, I’m visiting the Brown Theoretical Physics Center, hosted by Brad Marston.
I’m excited to chat with all of the great fluid dynamicists here and hopefully start some new lines of research.
In fact, that’s already happened. In my second week at Brown, who comes to visit? None other than Professor Alexander Morozov from the University of Edinburgh, one of the world’s foremost experts on elastic turbulence, and a keen user of Dedalus.
Some time ago, I’d been working on some biophysics problems in Dedalus, and I’d implemented the Oldroyd-B model for viscoelasticity.
The Oldroyd-B model is one of the simplest models of viscoelasticity, but that’s not saying much. It’s pretty complicated, and adds a tensor field, called the conformation tensor to the usual Navier-Stokes equations of fluid motions (which are kind of complicated all by themselves). In our new, still-beta version of Dedalus, known to its friends and family as d3, we have added the ability to handle vector and tensor fields, including all of their algebra and calculus. This means the code for solving the Oldroyd-B model becomes just a few lines:
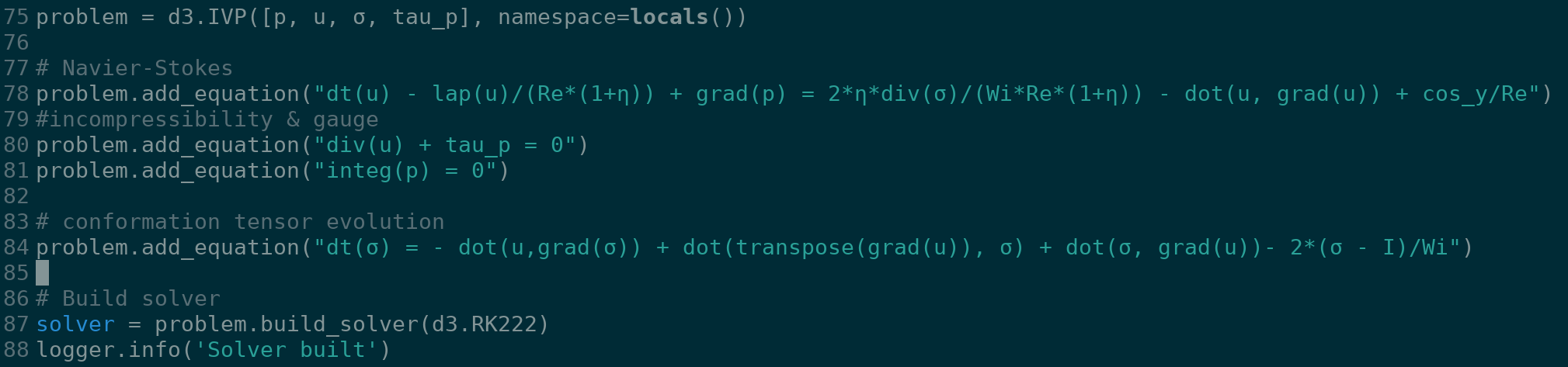
Anyway, I wanted to make sure my implementation was working, so I decided to test it on the viscoelastic Kolomogorov flow, which shows an elastic instability even when the non-viscoelastic flow would be stable. This is described in a great paper by Berti and Boffetta (Phys Rev E 2010), so I set out to reproduce their figure 2, which shows where the instability sets in as a function of Weissenberg number (Wi). If you look closely at the above image, you’ll see that there are three dimensionless parameters, Re, Wi, and η. However, the 2010 paper only reports Re and Wi! What is η? I couldn’t reproduce the results without it.
η is an unusual parameter, essentially telling you how much the viscoelastic component contributes to the total viscosity. It’s not at all obvious (to me, anyway) what value it should take. 1 is always a good guess, but that didn’t seem to work. This is a pretty common situation: you have a great result you want to reproduce, but the paper doesn’t always have all the details. While we all strive for reproducability, it can be easy to forget a parameter, particularly one that you don’t vary in your study! In fact, right now I have a referee report in my inbox that helpfully points out an important parameter I left out of my latest manuscript. It’s easy to do.
But rather than curse the darkness, there are many options. First, I could email the authors. Now, I had a few hours before Prof. Morozov was to show up in my office, so it was unlikely that they would get back to me in time. Next, I could redo the linear analysis for some value of η, find the instability threshold, and use that to test the simulation. But that also takes time to get right, and given that that requires the linearized form of the very same equations I’m trying to test, isn’t entirely unbiased. But there’s also a paper trail. In particular, Professor Boffetta had published a paper in 2005 on the linear stability of this system. Maybe that reported η…and indeed it did! Once I used that parameter value (η = 0.3, for the record), we got what we were looking for:
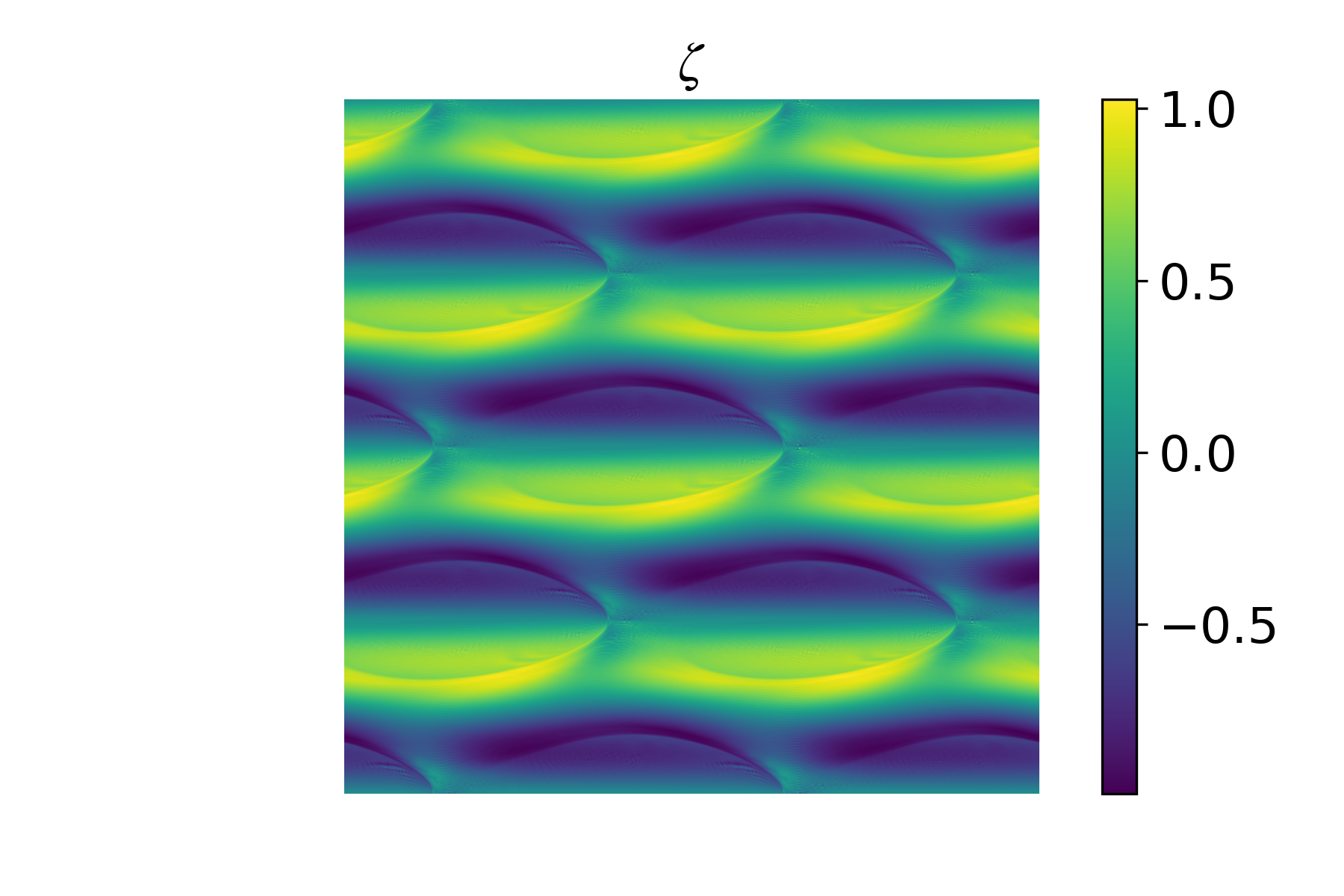
More soon to come…